Introduction
Machine vibration analysis is used in predictive maintenance to check machinery health and predict their failure. When performed regularly (or continuously) machine faults can be detected in their early stages and appropriate action can be taken to avoid machine failure or in the opposite end, replacing parts that are still in good condition (preventive maintenance).
Rotating machines generate vibration that can be analyzed to asses the general condition of machines and the remaining life of their parts. Vibration signature analysis can detect faults such as bearing faults, unbalance, misalignment and gear faults.
Bearings contain 4 elements that can deteriorate with the usage: the inner and outer race, the balls and the cage. Each of these elements generates a characteristic vibration frequency when faulty, making it in this way possible to identify the fault by just by analyzing the vibration signature.
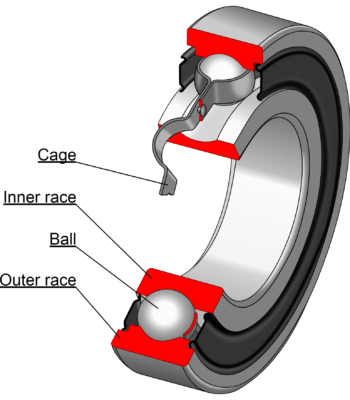
The frequencies are:
- BPFO (Ball Pass Frequency Outer): Number of balls or rollers that pass through a given point of the outer race each time the shaft makes a complete turn.
- BPFI (Ball Pass Frequency Inner): Number of balls or rollers that pass through a given point of the inner race each time the shaft makes a complete turn.
- BSF (Ball Spin Frequency): Number of turns that a bearing ball or roller makes each time the shaft makes a complete turn.
- FTF (Fundamental Train Frequency): Number of turns that makes the bearing cage each time the shaft makes a complete turn.
The exact frequencies depend on the physical properties of the bearings, such as the dimensions and the number of balls or rollers.
In this post I will show how a piezo-accelerometer sensor (Kemet VS-BV203) can be used to perform vibration analysis of a brushless motor (Sunnysky v2216-12 kv800 ii) to detect vibration generated by its bearings.
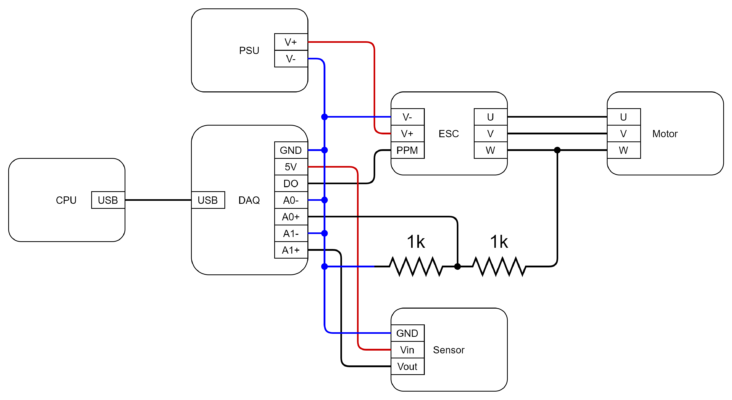
Hardware Setup
The setup was made of 5 components: A piezo-accelerometer/vibration sensor, a brushless DC motor (BLDC), an electronic speed control (ESC), a power supply (PSU), a data acquisition device (DAQ) and a computer.
The CPU controls the motor speed by setting the PSU voltage (from 6 to 16 V) and by controlling the ESC through a throttle PPM signal. The DAQ measures 2 signals, a vibration signal from the sensor and the voltage signal from a motor phase (which is used to compute the motor rotational frequency).
The physical setup was far from ideal, but good enough to experiment with, in a “real” setup much more care would have to be taken with the cabling and connections to avoid noise from leaking in. Due to the fast acceleration of the motor I had to attach it to a more rigid structure to avoid having it spin around the bench. The small size of the motor made it hard to attach the sensor directly to it, so I ended up attaching it to the structure to which the motor was tied to (this again was not ideal as the plastic cable ties dampen the motor vibration).
The DAQ (NI myDAQ) supports a maximum sampling frequency of 200 ksps @16 bit in the range of ±10 V, so I had to voltage divide the motor phase signal.
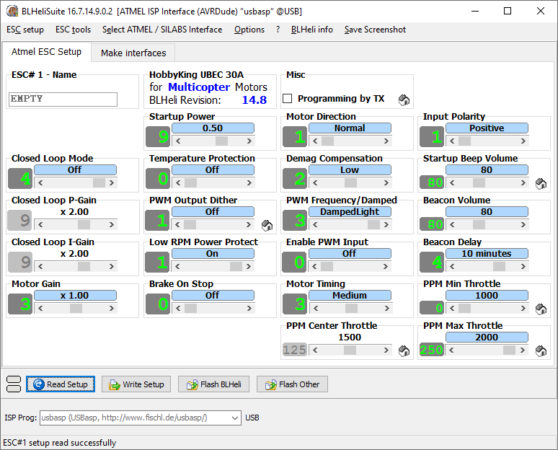
I reprogrammed the ESC with the BLHeli firmware and disabled its PID control loop and set the min and max PPM throttle values to 1000 and 2000 ms respectively (so that it would be easier to fine control its speed).
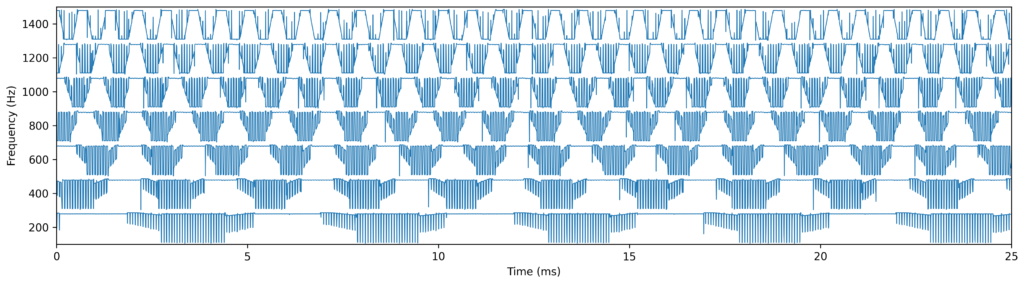
To test that all connections were properly set and that the motor was properly tightened, I performed a linear acceleration/deacceleration test:
Signal Processing
The key components of the project were the signal processing algorithms: tthe rotation tracker and the order tracker.
Rotation Tracking
The motor rotations were tracked by measuring the divided voltage signal of a single motor phase. The brushless motor that I used rotates one time for every 7 electrical cycles (the number of electrical cycles/rotations equals the rotor pole pairs). The processing of the signal was not trivial as the “form” the cycles depend on the frequency.
Due to the irregularity of the signal, simple approaches to track rotations such as identifying blocks without voltage “spikes” did not work. I implemented the rotation tracking algorithm as a sequence of the following operations:
- A high time resolution, low frequency resolution spectrogram is computed from the original signal.
- The main frequency at each segment of the spectrogram is computed and then interpolated at every time unit of the original signal.
- A filter bank of 5 bands ([100; 312.5], [312.5; 625], [625; 1250], [1250; 2500] and [2500; 5000] Hz) is created (the selected range includes up to the third harmonic of the signal).
- The filter bank is applied to the original signal to generate 5 filtered signals.
- The 5 filtered signals are linearly combined at each time unit based on the computed main frequency at each time unit.
- The linearly combined signal is used to detect all zero crossings with a negative derivative.
- Zero crossings were the signal amplitude is below a certain threshold are discarded.
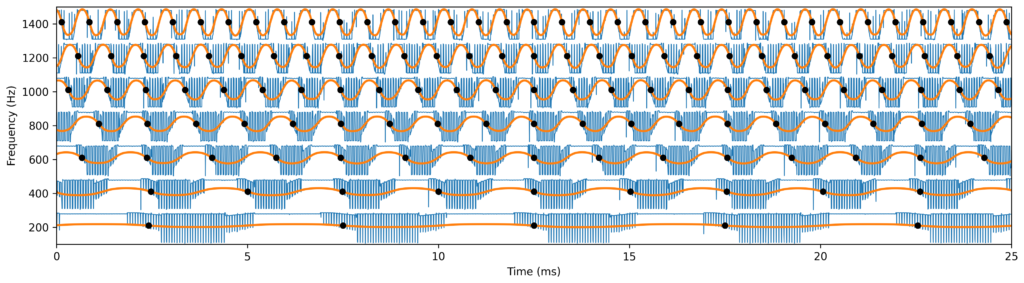
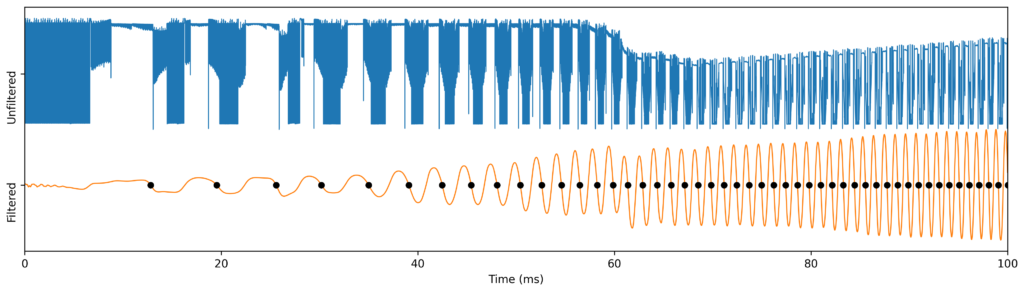
The next image shows the algorithm applied to the previous signal segments. The orange signal is the linearly combined signal and the dots are the negative derivative zero crossings.
The filter operates as a variable frequency lowpass filter that adapts to the signal main oscillation frequency. The next image shows how it adapts to a fast accelerating signal.
Order Tracking
Order tracking is a technique that can separate the synchronous vibration from the asynchronous vibration (the synchronous vibration frequency is proportional to the shaft rotational frequency, while the asynchronous vibration frequency is not). What the algorithm does is to convert a time series (a sequence of data points taken at successive equally spaced time units) into a rotational series, a series of equally spaced rotational increments of a reference shaft.
I implemented the algorithm in the following way:
- The vibration time series is expanded through FFT resampling.
- Rotational tracking is used to compute the negative derivative zero crossings.
- The computed zero crossings time locations are resampled to small rotational increments.
- The expanded vibration time series is sampled at the resampled small rotational increments (step 2).
The next synthetic time series shows an acceleration from 25 to 175 Hz of an unbalanced system (black points are used as a visual aid to separate rotations).
Through order tracking, the previous time series gets converted from the time domain to the rotation domain.
Experiments
As I could not find the exact bearing models of the motor, I focused the project on identifying the synchronous and asynchronous vibration components and implementing a real-time vibration analysis dashboard.
Signal Analysis
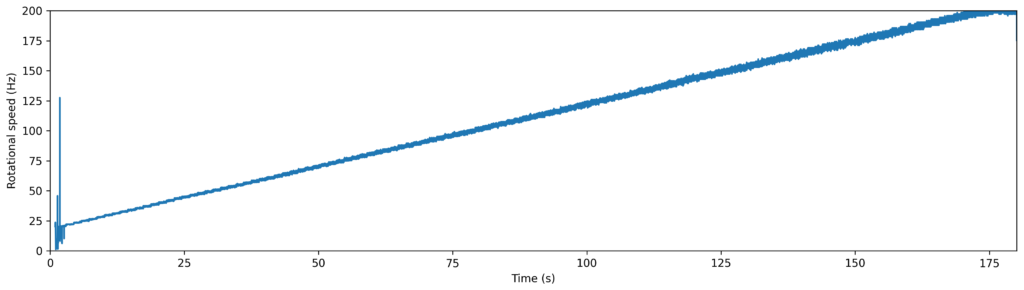
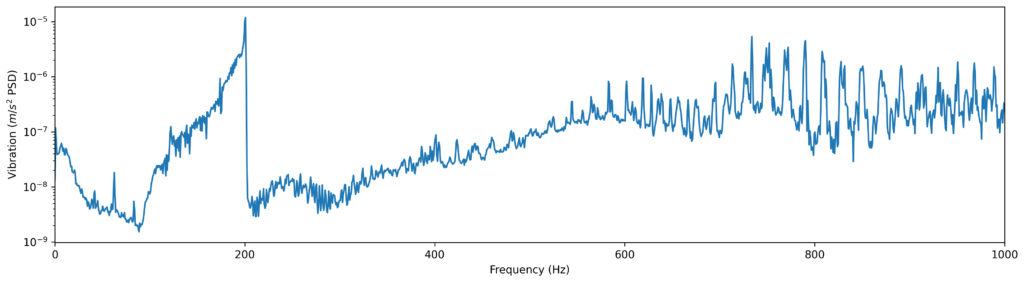
To identify which vibration components are asynchronous and which are synchronous I performed a relatively linear ~180 s sweep from ~20 Hz to ~200 Hz. The sweep highlights which spectrum components are affected by the shaft rotational frequency, and which are not, but it also helps with identifying synchronous components that could get damped at certain frequencies.
Through rotational tracking I measured the rotational frequency curve.
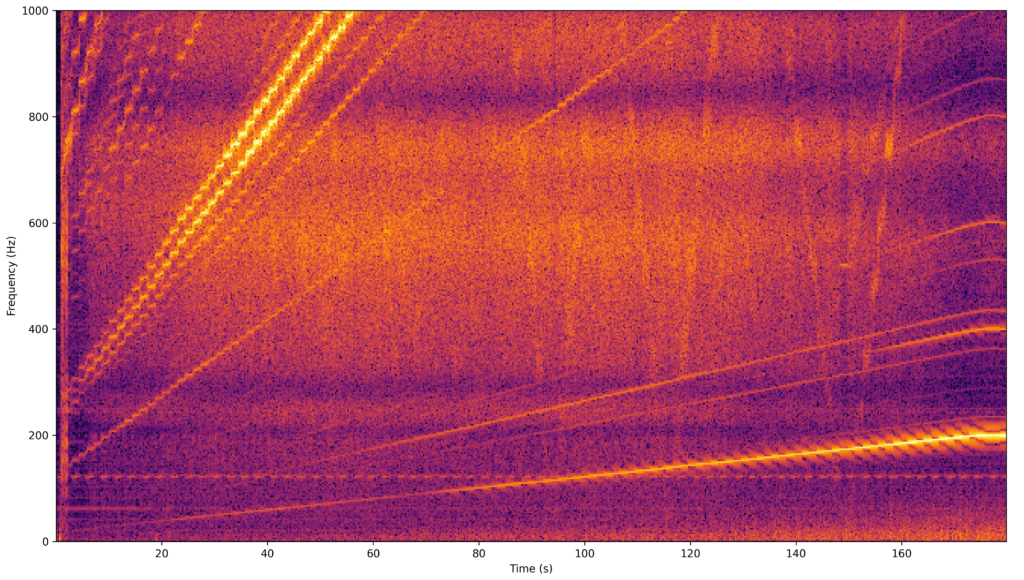
The sweep generated the next vibration frequency domain spectrogram.
The spectrogram shows asynchronous components as horizontal lines, and synchronous components as diagonal lines that scale with the rotational frequency by a constant factor (order). By computing the spectrogram of the order tracked signal, the synchronous components order frequency can be easily identified.
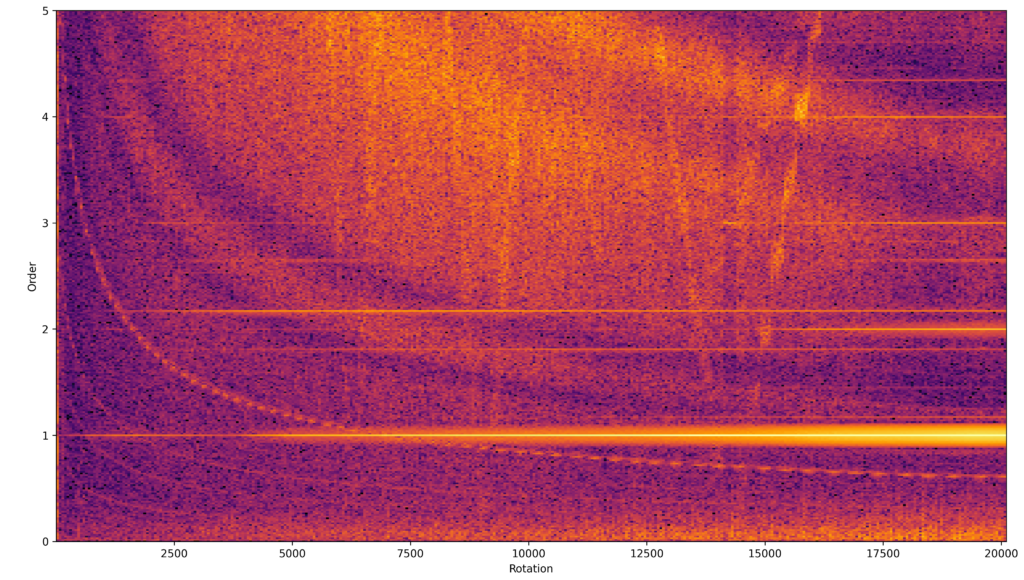
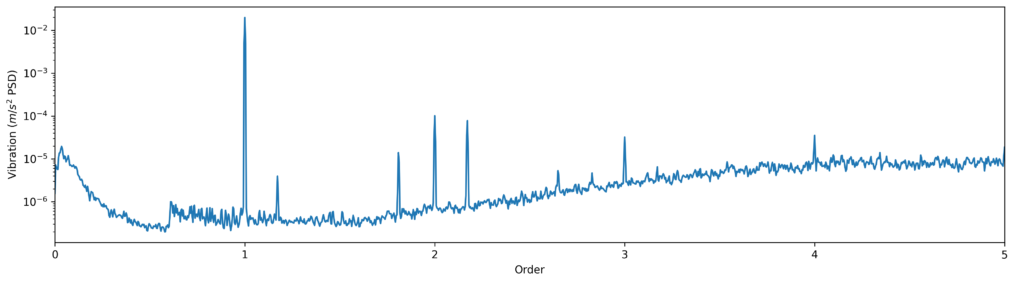
In contrast to the vibration frequency domain spectrogram, in the vibration order frequency domain, the synchronous components are shown as horizontal lines and the asynchronous components as decreasing curves.
The computation of the spectrum of the complete sweep highlights the components that stay constant in each domain, asynchronous in the frequency domain, and synchronous in the order domain.
Vibrations generated by bearings tend not to be in the frequency of the shaft rotation harmonics. The order spectrum shows a few frequency components that were likely generated by the bearings, but without the specification of the bearings I was not able to identify the bearing element faults. The motor that I used was new and its bearings were supposed to be of good quality, so it appears that the system is capable of detecting faults in the very early stages.
Real-time Dashboard
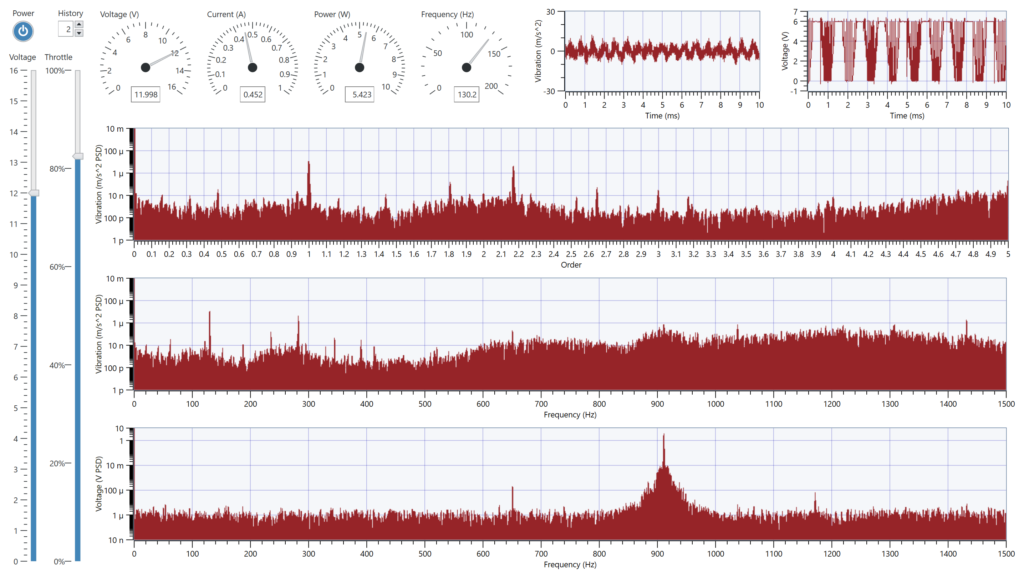
I chose LabVIEW to build a real-time vibration analysis system as it can easily integrate my NI DAQ and also supports Python. After integrating the Python rotation and order tracking functions into my LabVIEW program, I found that LabVIEW could not process the data fast enough. I ended up removing the Python code from the LabVIEW program and performed a simpler analysis that assumed constant rotational frequency during short time spans.
The dashboard contained 4 controls: A power button to turn on the PSU (accessed through VISA drivers), a voltage slide bar to set the PSU output voltage, a throttle slider that controls the ESC (through a PPM signal) and a history control, to set the size (in seconds) of the FFT window. The gauge indicators indicate the PSU readback voltage, current and power, and the motor oscillating frequency (the highest frequency component of phase signal spectrum). At the right there are two time domain plots to see the vibration and phase signal. And taking most of the dashboard space, the horizontal frequency domain plots show the order vibration spectrum, the frequency vibration spectrum and the phase voltage spectrum.
The next video shows how the system performs real-time analysis with constant and variable rotational frequency.
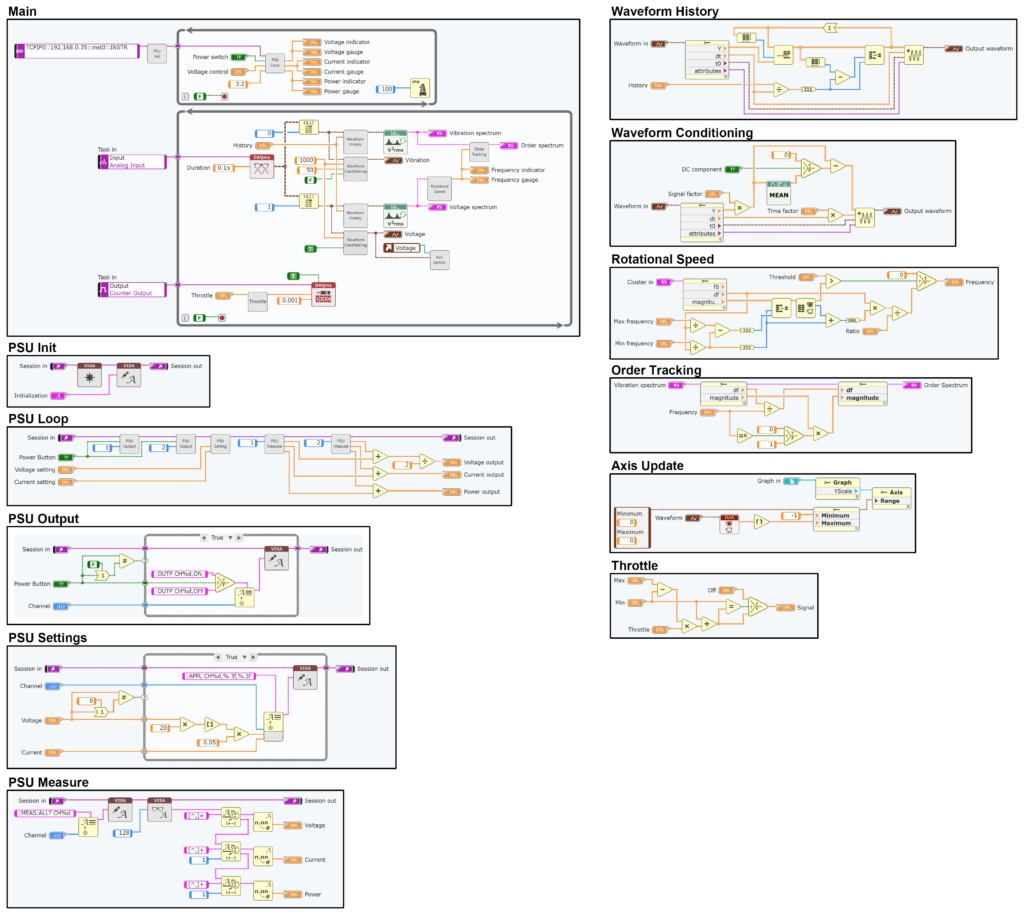
And just for completion’s sake, here are the modules that I built to create the system.
Conclusion
Vibration analysis is great tool to test the health of machines and perform predictive maintenance. The field of vibration analysis is huge, so here I just focused in a single method: order tracking, which is used to detect faults in rotating machinery such as motors and engines. The programming of the rotational tracker was what took me most of the time to develop, after a couple of failed approaches I developed an adaptive filter which ended up working great, but at a high computational cost. The order tracking algorithm itself was much easier to implement, and also less computationally expensive.
Even though I made sure that the algorithms would be able to process data in a fraction of the recorded time span (it could easily keep up with the dataflow), LabVIEW was not able to run the code smoothly. I’m not completely sure why this happened, but I suspect that through some tweaking it may still be possible to implement the Python code into the system.
Taking into account the price of the sensor and digitizing systems in comparison to expensive motors and engines, it may be a good idea to permanently attach vibration sensors to rotating machinery to continuously track the health of the machine. Eventually in the future, as machines get smarter, they will begin to implement their own vibration analysis system to track their own health and evolution of faults.
The code is available on GitHub